layout: true class: typo, typo-selection --- count: false class: nord-dark, middle, center # ☯ Primal-Dual Method for Approximation Algorithms @luk036 👨‍💻 · 2026 📅 [](https://netlistx.readthedocs.io/en/latest/?badge=latest) [](https://codecov.io/gh/luk036/netlistx) --- ## 📝 Abstract The primal-dual method is a powerful technique in the field of approximation algorithms. Originating from linear programming and combinatorial optimization, it has been adapted to tackle NP-hard problems effectively. This lecture explores the fundamentals, methodology, and applications of this versatile approach, demonstrating its significance in developing efficient solutions for complex computational challenges that would otherwise be intractable. --- ### 🧮 Fundamentals of the PD Method - Dual Approach 🔄: The primal-dual method considers both the primal integer programming formulation and the dual of its LP relaxation. This dual perspective provides valuable insights into the problem structure. - Iterative Improvement 🔁: Starting with a dual feasible solution, the method iteratively improves while constructing a primal integral solution. This process often leads to dual-ascent algorithms. - Relaxed Conditions ⚖️: For NP-hard problems, the method relaxes complementary slackness conditions, allowing for efficient approximation algorithms with provable guarantees. --- ### 📚 Example: Vertex Cover - Instance: A graph $G = ({\color{salmon}V}, {\color{lime}E})$ - Solution: A vertex cover for $G$, i.e., a subset ${\color{salmon}U}$ such that, for each edge $(u,v) \in {\color{lime}E}$, at least one of $u$ and $v$ belongs to ${\color{salmon}U}$ 🛡️ - Measure: Cardinality of the vertex cover, i.e. $|{\color{salmon}U}|$ 📏 - Bad News: APX-complete. 😟 - Comment: Admits a PTAS for *planar* graphs [Baker, 1994]. The generalization to $k$-hypergraphs, for $k>1$, is approximable within $k$ [Bar-Yehuda and Even, 1981] and [Hochbaum, 1982a]. 📖 - Garey and Johnson: GT1 📚 --- ### ⚙️ Greedy-Vertex-Cover ```text ┌─┬─────────────────────────────────────────┐ │1│U = {} │ │2│do chose v in V with max. degree │ │3│ U = U + {v} │ │4│ remove v and every edge adjacent to v│ │5│until all edges covered │ │6│return U │ └─┴─────────────────────────────────────────┘ ``` Requirements: - Need a (bucket) heap to maintain max. degree ⚖️ - Only for unweighted problems. 🏋️‍♂️ --- ### ⚖️ Weighted Vertex Cover (WVC) The Weighted Vertex Cover problem extends the basic vertex cover by assigning weights to vertices. - Instance: $G = ({\color{salmon}V}, {\color{lime}E})$ with non-negative vertex weights ${\color{coral} w}: {\color{salmon}V} ↦ N$ 🏷️ - Solution: A vertex cover for $G$, i.e., a subset ${\color{salmon}U}$ such that, for each edge $(u,v) ∈ {\color{lime}E}$, at least one of $u$ and $v$ belongs to ${\color{salmon}U}$ 🛡️  This problem has applications in network monitoring, resource allocation, and conflict resolution in scheduling. 🌐 --- ### 🧮 Mathematical Formulation of WVC ILP Formulation: $$\begin{array}{lll} \text{minimize} & \sum_{v \in {\color{salmon}V} } {\color{coral} w}_v {\color{green} x}_v \\ \text{subject to} & {\color{green} x}_u + {\color{green} x}_v \geq 1, & \forall (u, v) \in {\color{lime}E} \\ & {\color{green} x}_v \in \{0, 1\}, & \forall v \in {\color{salmon}V} \end{array}$$ LP Relaxation: .pull-left[ Primal LP: $$\begin{array}{lll} \text{min} & \sum_{v \in {\color{salmon}V} } {\color{coral} w}_v {\color{green} x}_v \\ \text{s.t.} & {\color{green} x}_u + {\color{green} x}_v \geq 1, & \forall (u, v) \in {\color{lime}E} \\ & 0 \leq {\color{green} x}_v \leq 1, & \forall v \in {\color{salmon}V} \end{array}$$ ] .pull-right[ Dual LP: $$\begin{array}{lll} \text{max} & \sum_{e \in {\color{lime}E} } {\color{firebrick} y}_e \\ \text{s.t.} & \sum_{e \in \text{adj}(v)} {\color{firebrick} y}_e \leq {\color{coral} w}_v, & \forall v \in {\color{salmon}V} \\ & {\color{firebrick} y}_e \geq 0, & \forall e \in {\color{lime}E} \end{array}$$ ] --- ### ⚙️ Primal-Dual Algorithm for WVC - Initialize 🏁 Set all dual variables to zero. Start with empty vertex cover ${\color{salmon}U}$. - Find Uncovered Edge 🔍 Locate an edge $e=(u,v)$ not yet covered by ${\color{salmon}U}$. - Increase Dual Variable 📈 Increase ${\color{firebrick} y}_e$ until a dual constraint becomes tight. - Add Vertex ➕ Add the vertex with tight constraint to the cover ${\color{salmon}U}$. --- ### ⚙️ Primal-dual WVC - **Input** Graph $G = ({\color{salmon}V}, {\color{lime}E})$ with non-negative vertex weights ${\color{coral} w}$ - **Output** Vertex cover ${\color{salmon}U}$ of $G$ 🛡️ - Let DLP_VC be the dual of the LP relaxation of ILP_VC ⚖️ - ~~**for** each dual variable $y$ of DLP_VC **do** $y$ := 0;~~ - ${\color{salmon}U} := 0$ 🏁 - **while** ${\color{salmon}U}$ is not a vertex cover **do** 🔁 - Let $e = (u, v)$ be an edge not covered by ${\color{salmon}U}$ 🔍 - Increase ${\color{firebrick} y}_e$ until a constraint of DLP_VC becomes tight 📈 - **if** $\sum_{e \in {\color{lime}E} } {\color{firebrick} y}_{e}$ is tight **then** ⚖️ - ${\color{salmon}U} := {\color{salmon}U} \cup \{u\}$ ➕ - **else** - ${\color{salmon}U} := {\color{salmon}U} \cup \{v\}$ ➕ - **return** ${\color{salmon}U}$ 🎯 --- ### 🐍 Python Implementation ```python def min_vertex_cover(ugraph, weight, coverset = None): if coverset is None: coverset = set() total_dual_cost = 0 # for assertion total_prml_cost = 0 gap = copy.copy(weight) for utx, vtx in ugraph.edges(): if utx in coverset or vtx in coverset: continue if gap[utx] < gap[vtx]: utx, vtx = vtx, utx # swap coverset.add(vtx) total_dual_cost += gap[vtx] total_prml_cost += weight[vtx] gap[utx] -= gap[vtx] gap[vtx] = 0 assert total_dual_cost <= total_prml_cost return coverset, total_prml_cost ``` --- ### 🧠 General Methodology 1. Formulate as Integer Program 📝: Begin by expressing the problem as an integer programming formulation, capturing the essential constraints and objectives. 2. Consider LP Relaxation Dual ⚖️: Analyze the dual of the linear programming relaxation, which provides a lower bound on the optimal solution. 3. Iterative Improvement 🔁: Incrementally increase dual variables while constructing a primal solution, ensuring feasibility and optimality conditions are maintained. 4. Approximation Analysis 📊: Evaluate the approximation ratio based on the relationship between the constructed primal and dual solutions. --- ### 💪 Key Strengths of the PD Method - Provable Approximation Guarantees 💯: The method provides mathematically rigorous bounds on solution quality, ensuring reliable performance. - Combinatorial Algorithms 🧩: Often leads to efficient combinatorial algorithms, avoiding the need for solving large linear programs. - Problem Structure Insights 🔍: Offers deep insights into the underlying structure of complex optimization problems. - Wide Applicability 🌐: Suitable for a broad range of NP-hard problems across various domains of computer science and operations research. --- ### 🔄 Generic PD for Cover Problems 1. Initialize 🏁: Begin with an empty solution set $A$ and set all dual variables $y$ to 0. 2. Iterate 🔁: While the solution A is not feasible, identify violated connectivity requirements, increase corresponding dual variables, and add edges to $A$ when dual constraints become tight. 3. Prune ✂️: Remove unnecessary edges from $A$ to optimize the final solution. 4. Return Solution 🎯 Output the optimized solution with provable approximation guarantees based on the relationship between primal and dual values. --- ### 🐍 Python Implementation ```python def pd_cover( violate: Callable, weight, soln: Set ) -> Tuple[Set, Union[int, float]]: total_prml_cost = 0 total_dual_cost = 0 gap = copy.copy(weight) for S in violate(): min_vtx = min(S, key=lambda vtx: gap[vtx]) min_val = gap[min_vtx] soln.add(min_vtx) total_prml_cost += weight[min_vtx] total_dual_cost += min_val for vtx in S: gap[vtx] -= min_val assert total_dual_cost <= total_prml_cost return soln, total_prml_cost ``` --- ### 📚 Example: WVC for Hypergraph A hypergraph extends the concept of a graph by allowing edges to connect any number of vertices. The vertex cover problem for hypergraphs requires finding a minimum weight set of vertices that intersects with every hyperedge, making it more complex than the standard graph version. - Instance: $H = ({\color{salmon}V}, {\color{lime}E})$ with non-negative vertex weights ${\color{coral} w}: {\color{salmon}V} ↦ N$ 🏷️ - Solution: A vertex cover for $H$, i.e., a subset ${\color{salmon}U}$ such that, for each edge $e ∈ {\color{lime}E}$, at least one of adj($e$) belongs to ${\color{salmon}U}$ 🛡️  --- ### 🧮 Mathematical Formulation of WVC ILP Formulation: $$\begin{array}{lll} \text{minimize} & \sum_{v \in {\color{salmon}V} } {\color{coral} w}_v {\color{green} x}_v \\ \text{subject to} & \sum_{v \in \text{adj}(e)} {\color{green} x}_v \geq 1, & \forall e \in {\color{lime}E} \\ & {\color{green} x}_v \in \{0, 1\}, & \forall v \in {\color{salmon}V} \end{array}$$ LP Relaxation: .pull-left[ Primal LP: $$\begin{array}{lll} \text{min} & \sum_{v \in {\color{salmon}V} } {\color{coral} w}_v {\color{green} x}_v \\ \text{s.t.} & \sum_{v \in \text{adj}(e)} {\color{green} x}_v \geq 1, & \forall e \in {\color{lime}E} \\ & 0 \leq {\color{green} x}_v \leq 1, & \forall v \in {\color{salmon}V} \end{array}$$ ] .pull-right[ Dual LP: $$\begin{array}{lll} \text{max} & \sum_{e \in {\color{lime}E} } {\color{firebrick} y}_e \\ \text{s.t.} & \sum_{e \in \text{adj}(v)} {\color{firebrick} y}_e \leq {\color{coral} w}_v, & \forall v \in {\color{salmon}V} \\ & {\color{firebrick} y}_e \geq 0, & \forall e \in {\color{lime}E} \end{array}$$ ] --- ### 🐍 Python Implementation ```python def min_hyper_vertex_cover( hgr, weight, coverset = None ) -> Tuple[Set, Union[int, float]]: if coverset is None: coverset = set() def violate_netlist() -> Generator: for net in hyprgraph.nets: if any(v in coverset for v in hgr.ugraph[net]): continue yield hyprgraph.ugraph[net] return pd_cover(violate_netlist, weight, coverset) ``` --- ### 🔄 Weighted Cycle Cover (WCC) Find a minimum weight set of vertices that intersects with every cycle in the graph. This problem has applications in breaking feedback loops in systems and ensuring acyclic dependencies. - Instance: $G = ({\color{salmon}V}, {\color{lime}E})$ with non-negative vertex weights ${\color{coral} w}: {\color{salmon}V} ↦ N$ 🏷️ - Define: a cycle $c$ is a subset of ${\color{salmon}V}$ ... , $C$ is a set of all cycles 🔄 - Solution: A vertex cover for $G$, i.e., a subset ${\color{salmon}U}$ such that, for each cycle $c ∈ C$, at least one of vertices belongs to ${\color{salmon}U}$ 🛡️  --- ### 🧮 Mathematical Formulation of WCC ILP Formulation: $$\begin{array}{lll} \text{minimize} & \sum_{v \in {\color{salmon}V} } {\color{coral} w}_v {\color{green} x}_v \\ \text{subject to} & \sum_{v \in c} {\color{green} x}_v \geq 1, & \forall c \in C \\ & {\color{green} x}_v \in \{0, 1\}, & \forall v \in {\color{salmon}V} \end{array}$$ LP Relaxation: .pull-left[ Primal LP: $$\begin{array}{lll} \text{min} & \sum_{v \in {\color{salmon}V} } {\color{coral} w}_v {\color{green} x}_v \\ \text{s.t.} & \sum_{v \in c} {\color{green} x}_v \geq 1, & \forall c \in C \\ & 0 \leq {\color{green} x}_v \leq 1, & \forall v \in {\color{salmon}V} \end{array}$$ ] .pull-right[ Dual LP: $$\begin{array}{lll} \text{max} & \sum_{c \in C} {\color{firebrick} y}_c \\ \text{s.t.} & \sum_{c: v \in c} {\color{firebrick} y}_c \leq {\color{coral} w}_v, & \forall v \in {\color{salmon}V} \\ & {\color{firebrick} y}_c \geq 0, & \forall c \in C \end{array}$$ ] --- ### 🐍 Python Implementation ```python def min_cycle_cover( ugraph: nx.Graph, weight, coverset = None ) -> Tuple[Set, Union[int, float]]: if coverset is None: coverset = set() def find_cycle(): for info, parent, child in _generic_bfs_cycle( ugraph, coverset): return _construct_cycle(info, parent, child) def violate() -> Generator: while True: S = find_cycle() if S is None: break yield S return pd_cover(violate, weight, coverset) ``` --- ### 🔄 Weighted Odd Cycle Cover Find a minimum weight set of vertices that intersects with every odd-length cycle. This problem is equivalent to making a graph bipartite by removing vertices and has applications in conflict resolution. - Instance: $G = ({\color{salmon}V}, {\color{lime}E})$ with non-negative vertex weights ${\color{coral} w}: {\color{salmon}V} ↦ N$ 🏷️ - Define: an odd cycle $c$ is a subset of ${\color{salmon}V}$ ... , $C_\text{odd}$ is a set of all odd cycles 1️⃣3️⃣5️⃣ - Solution: A vertex cover for $G$, i.e., a subset ${\color{salmon}U}$ such that, for each odd cycle $c ∈ C_\text{odd}$, at least one of vertices belongs to ${\color{salmon}U}$ 🛡️  --- ### 🧮 Mathematical Formulation ILP Formulation of WOCC: $$\begin{array}{lll} \text{minimize} & \sum_{v \in {\color{salmon}V} } {\color{coral} w}_v {\color{green} x}_v \\ \text{subject to} & \sum_{v \in c} {\color{green} x}_v \geq 1, & \forall c \in C_\text{odd} \\ & {\color{green} x}_v \in \{0, 1\}, & \forall v \in {\color{salmon}V} \end{array}$$ LP Relaxation: .pull-left[ Primal LP: $$\begin{array}{lll} \text{min} & \sum_{v \in {\color{salmon}V} } {\color{coral} w}_v {\color{green} x}_v \\ \text{s.t.} & \sum_{v \in c} {\color{green} x}_v \geq 1, & \forall c \in C_\text{odd} \\ & 0 \leq {\color{green} x}_v \leq 1, & \forall v \in {\color{salmon}V} \end{array}$$ ] .pull-right[ Dual LP: $$\begin{array}{lll} \text{max} & \sum_{c \in C_\text{odd} } {\color{firebrick} y}_c \\ \text{s.t.} & \sum_{c: v \in c} {\color{firebrick} y}_c \leq {\color{coral} w}_v, & \forall v \in {\color{salmon}V} \\ & {\color{firebrick} y}_c \geq 0, & \forall c \in C_\text{odd} \end{array}$$ ] --- ### 🐍 Python Implementation ```python def min_odd_cycle_cover( ugraph, weight, coverset = None ) -> Tuple[Set, Union[int, float]]: if coverset is None: coverset = set() def find_odd_cycle(): for info, parent, child in _generic_bfs_cycle( ugraph, coverset): _, depth_child = info[child] _, depth_parent = info[parent] if (depth_parent - depth_child) % 2 == 0: return _construct_cycle(info, parent, child) def violate() -> Generator: while True: S = find_odd_cycle() if S is None: break yield S return pd_cover(violate, weight, coverset) ``` --- ### 🏭 Applications in EDA WOCC is used in Electronic Design Automation for Double Patterning Lithography (DPL) combined with E-beam lithography, solving coloring conflicts in semiconductor manufacturing. 🖥️🔬 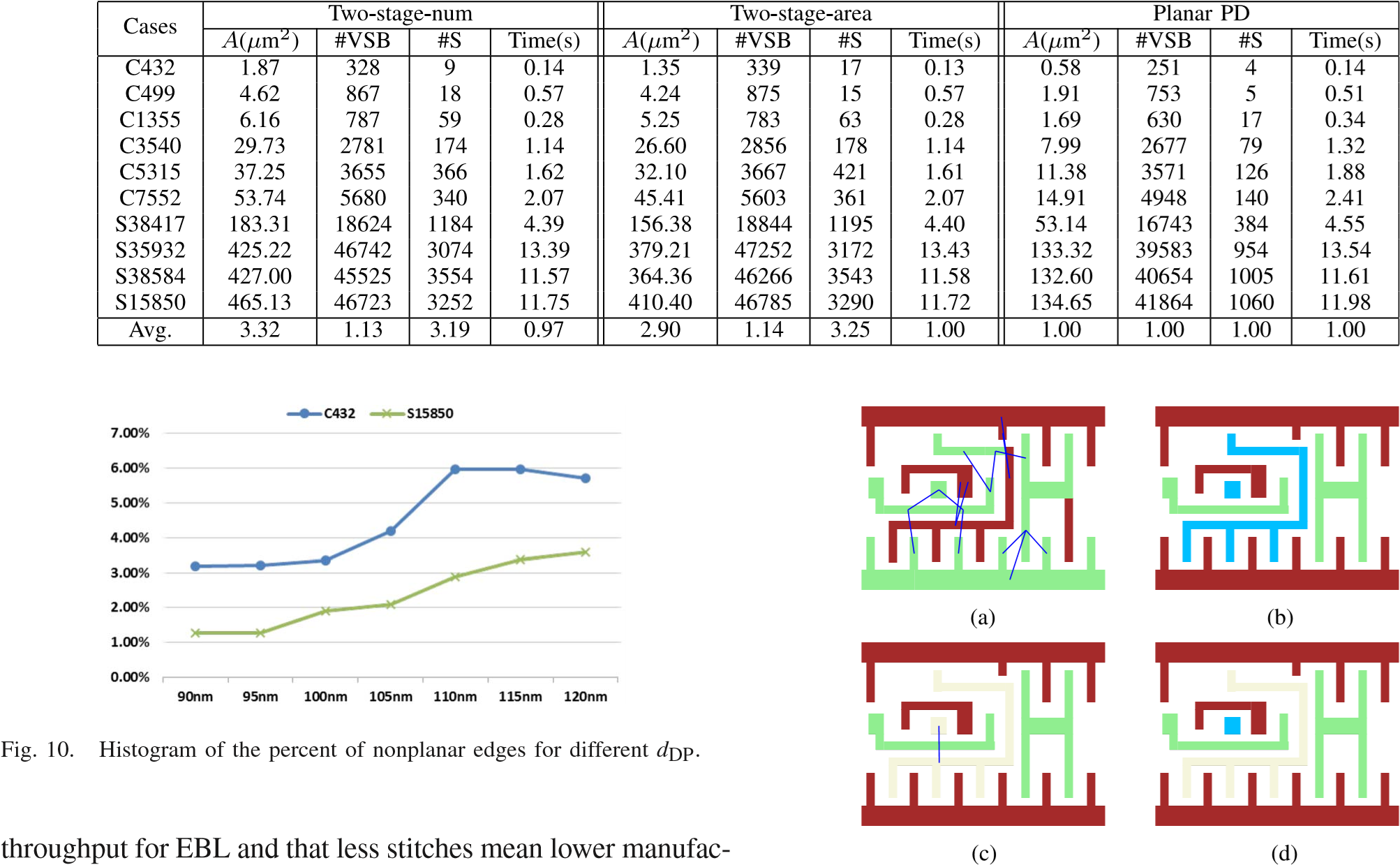 ---  --- ### 🧩 Weighted Maximal Matching (WMM) for Hypergraph - Instance: $H = ({\color{salmon}V}, {\color{lime}E})$ with non-negative vertex weights ${\color{coral} w}: {\color{salmon}V} ↦ N$ 🏷️  - Application: clustering 🧩 --- ### 🧮 LP Relaxation of WMM Primal LP: $$\begin{array}{lll} \text{min} & \sum_{e \in {\color{lime}E} } {\color{coral} w}_e {\color{green} x}_e \\ \text{s.t.} & \sum_{e \in \text{adj}(v)} {\color{green} x}_e \leq 1, & \forall v \in {\color{salmon}V} \\ & {\color{green} x}_e + \sum_{v \in \text{adj}(e)} \sum_{f \in \text{adj}(v)} {\color{green} x}_f \geq 1, & \forall e \in {\color{lime}E} \\ & 0 \leq {\color{green} x}_v \leq 1, & \forall v \in {\color{salmon}V} \end{array}$$ Dual LP: $$\begin{array}{lll} \text{max} & \sum_{e \in {\color{lime}E} } {\color{firebrick} y}_e - \sum_{v \in {\color{salmon}V} } {\color{firebrick} z}_v \\ \text{s.t.} & {\color{firebrick} y}_e + \sum_{v \in \text{adj}(e)} (-{\color{firebrick} z}_v + \sum_{f \in \text{adj}(v)} {\color{firebrick} y}_f) \leq {\color{coral} w}_e, & \forall e \in {\color{lime}E} \\ & {\color{firebrick} y}_e \geq 0, & \forall e \in {\color{lime}E} \\ & {\color{firebrick} z}_v \geq 0, & \forall v \in {\color{salmon}V} \end{array}$$ --- ### 🐍 Python Implementation .font-sm.mb-xs[ ```python def min_maximal_matching(hyprgraph, weight, matchset, dep): def cover(net): for vtx in hyprgraph.ugraph[net]: dep.add(vtx) def any_of_dep(net): return any(vtx in dep for vtx in hyprgraph.ugraph[net]) total_prml_cost = 0 gap = copy.copy(weight) for net in hyprgraph.nets: if any_of_dep(net): continue if net in matchset: continue # pre-define matching min_val = gap[net] min_net = net for vtx in hyprgraph.ugraph[net]: for net2 in hyprgraph.ugraph[vtx]: if any_of_dep(net2): continue if min_val > gap[net2]: min_val = gap[net2] min_net = net2 cover(min_net) matchset.add(min_net) total_prml_cost += weight[min_net] if min_net == net: continue gap[net] -= min_val for vtx in hyprgraph.ugraph[net]: for net2 in hyprgraph.ugraph[vtx]: gap[net2] -= min_val assert total_dual_cost <= total_prml_cost return matchset, total_prml_cost ``` ] --- ### 🌐 Other Applications and Extensions - 🌳 Steiner Tree Problem: Connect a subset of vertices at minimum cost, a fundamental problem in network design. - 🛡️ Survivable Network Design: Design networks resilient to failures, ensuring connectivity under various scenarios. - 📶 Wireless Network Design: Design wireless networks with limited resources, optimizing coverage and capacity. --- ### Primal-Dual Method Flow 🔄 .mermaid[ <pre> graph LR A(Start) --> B(Primal Solution) B --> C(Dual Solution) C --> D{Check Gap} D -->|Not Approx.| B D -->|Approx. Optimal| E(Approximation) style A fill:#4caf50 style B fill:#2196f3 style C fill:#ff9800 style D fill:#9c27b0 style E fill:#f44336 </pre> ] --- ### 🎯 Conclusion The primal-dual method stands as a significant technique in the field of approximation algorithms. Its ability to provide provable performance guarantees through a systematic approach based on linear programming duality makes it invaluable for tackling a wide array of NP-hard optimization problems. The method's success in areas like vertex cover problems, cycle cover problems, network design, and electronic design automation underscores its versatility and practical importance. By offering both theoretical guarantees and often leading to efficient combinatorial algorithms, the primal-dual method continues to be a crucial tool for addressing complex computational challenges. --- count: false class: nord-dark, middle, center .pull-left[ ## Q&A 🎤 ] .pull-right[  ]