Projective Geometry in 1D

👋 Introduction

🔑 Key points

A simplified version of the projective plane.
Möbius transformation can be viewed as a projective transform of a complex projective point.

Projective Line's Basic Elements

Projective Line Concept

Only involve "Points".
"Points" is assumed to be distinguishable.
Denote $A$ = $B$ as $A$ and $B$ are referred to the same point.
E.g., $(1/3)$ = $(10/30)$
We have the following rules:
- $A$ = $A$ (reflective)
- If $A$ = $B$ , then $B$ = $A$ (symmetric)
- If $A$ = $B$ and $B$ = $C$ , then $A = C$ (transitive)
Unless mention specifically, objects in different names are assumed to be distinct, i.e. $A \neq = B$ .

Homogenous Coordinates

Let $v_{1} = [x_{1}, y_{1}]$ and $v_{2} = [x_{2}, y_{2}]$ .
- dot product $v_{1} \cdot v_{2}$ = $v_{1}^{T} v_{2}$ = $x_{1} x_{2} + y_{1} y_{2}$ .
- cross product $v_{1} \times v_{2}$ = $x_{1} y_{2} - y_{1} x_{2}$
Then, we have:
- $A = B$ if and only if $[A] \times [B] = 0$
Example: the point $(5/10)$ and $(3/6)$ is the same because $5 \cdot 6 - 3 \cdot 10 = 0$
The cross product is also used as a basic measure between two points.
The cross ratio of four points $R_{1} (a, b; c, d)$ is given by: $R_{1} (a, b; c, d) = (a \times c) (b \times d) / (a \times d) (b \times c)$

Example 1: Euclidean Geometry

Point: projection of a 2D vector $p = [x, y]$ to 1D line $y = 1$ : $(x^{'}) = (x / y)$
$p_{\infty} = [x, 0]$ is a point at infinity.
$[0, 0]$ is not a valid point.

Example 1: Euclidean Geometry (measurement)

The quadrance $Q$ between points $A_{1}$ and $A_{2}$ is: $Q = (x_{1}^{'} - x_{2}^{'})^{2} = (x_{1} / y_{1} - x_{2} / y_{2})^{2}$
Let $A_{1}$ , $A_{2}$ and $A_{3}$ are points with $Q_{1} \equiv Q (A_{2}, A_{3})$ , $Q_{2} \equiv Q (A_{1}, A_{3})$ and $Q_{3} \equiv Q (A_{1}, A_{2})$ .
TQF (Triple quad formula): $(Q_{1} + Q_{2} + Q_{3})^{2} = 2 (Q_{1}^{2} + Q_{2}^{2} + Q_{3}^{2})$
TQF (non-symetric form): $(Q_{1} + Q_{2} - Q_{3})^{2} = 4 (Q_{1} Q_{2})$

Euclidean 1D plane from 2D vector

<!--
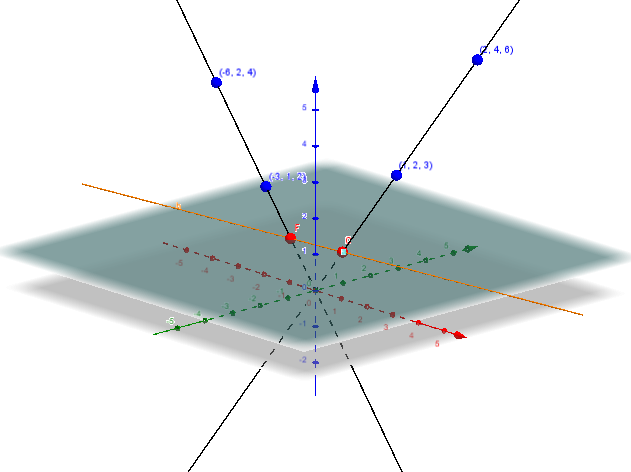![](figs/euclidean.png){#fig:euclidean}
-->

Example 2: Elliptic Geometry

"Point": projection of 2D vector $[x, y]$ to the unit circle. $(x^{'}, y^{'}) = (x / r, y / r)$

where $r^{2} = x^{2} + y^{2}$ .
Two points on the opposite poles are considered the same point here.

Example 2: Elliptic Geometry (measurement)

The measure of two points is the "spread" of the point.
The spread $S$ between points $A_{1}$ and $A_{2}$ is: $s (A_{1}, A_{2}) = 1 - (x_{1} x_{2} + y_{1} y_{2})^{2} / (x_{1}^{2} + y_{1}^{2}) (x_{2}^{2} + y_{2}^{2})$
Let $A_{1}$ , $A_{2}$ and $A_{3}$ are points with $S_{1} \equiv S (A_{2}, A_{3})$ , $S_{2} \equiv S (A_{1}, A_{3})$ and $S_{3} \equiv S (A_{1}, A_{2})$ .
TSF (Triple spread formula): $(S_{1} + S_{2} + S_{3})^{2} = 2 (S_{1}^{2} + S_{2}^{2} + S_{3}^{2}) + 4 S_{1} S_{2} S_{3} .$

<!--
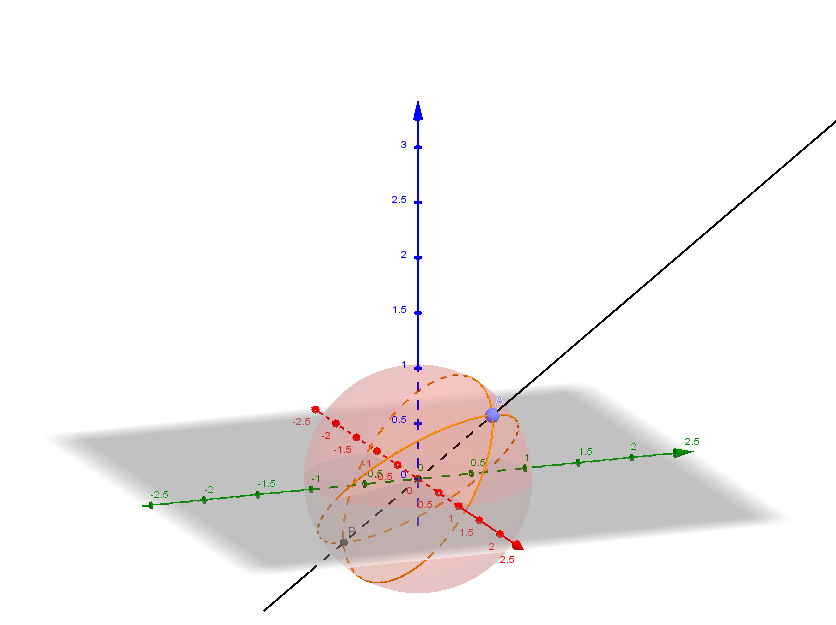![](figs/sphere.png){#fig:sphere}
-->

Example 4: Hyperbolic Geometry

A velocity "point": projection of a 2D vector $[p] = [x, t]$ to 1D line $t = 1$ : $(v) = (x / t)$
The measure of two velocity points is the relative speed of two points.

$Speed (p, q) = (x_{p} t_{q} - t_{p} x_{q})^{2} / (x_{p}^{2} - t_{p}^{2}) (x_{q}^{2} - t_{q}^{2}) = (v_{p} - v_{q})^{2} / (v_{p}^{2} - 1) (v_{q}^{2} - 1)$

Assume that the speed of light is normalized as 1. Then Speed( $p$ , $q$ ) can never exceed 1 when $∣ v_{p} ∣ \leq 1$ and $∣ v_{q} ∣ \leq 1$ .

Projective Transformation

Given a nonsingular matrix $T$ = $[a c b d]$ . The transformation $[x^{'}, y^{'}] = τ ([x, y]) = [a x + b y, c x + d y]$
Let $z = x / y$ , the formula becomes: $z^{'} = (a z + b) / (cz + d)$
This is exactly the Möbius transformation, where $z$ is a complex number.
Möbius transformation plays an important role in the electromagetic theory.
There are two fixed points in this transformation, considering infinity as also a fixed point.