Projective Geometry

👋 Introduction

Geometry and Algebra

• Geometry
  • Points, lines, triangles, circles, conic sections...
  • Collinear, concurrent, parallel, perpendicular...
  • Distances, angles, areas, quadrance, spread, quadrea...
  • Midpoint, bisector, orthocenter, pole/polar, tangent...
• Algebra
  • Addition, multiplication, inverse...
  • Elementary algebra: integer/rational/real/complex... numbers.
  • Abstract Algebra: rings, fields...
  • Linear algebra: vector, matrix, determinant, dot/cross product...
• The two subjects are linked by coordinates.

🔑 Key points

• The earth is not flat and our universe is non-Euclidean.

• Non-Euclidean geometry is much easier to learn than you might think.

• Our curriculum in school is completely wrong.

• Euclidean geometry is asymmetric. Three sides determine a triangle, but three angles do not determine a triangle. This may not the case in general geometries. Euclidean geometry is just a special case.

• Yet Euclidean geometry is computationally more efficient and is still used in our small-scale everyday life.

• Incidenceship facilitates integer arithmetic; non-oriented measurement facilitates rational arithmetic; oriented measurement facilitates floating-point arithmetic. Don't shoot rabbits with machine guns.

The Basic Elements of Projective Plane

The concept of Projective Plane

• Only "points" and "lines" are involved.

• Assume that "points" (or "lines") are distinguishable.

• Denote $A$ = $B$ as $A$ and $B$ refer to the same point.

• E.g., $(1/3,2/3)$ = $(10/30,20/30)$

• We have the following rules:

  • $A$ = $A$ (reflective)
  • If $A$ = $B$, then $B$ = $A$ (symmetric)
  • If $A$ = $B$ and $B$ = $C$, then $A=C$ (transitive)

• Unless otherwise mentioned, objects with different names are assumed to be distinct, i.e. $A\ne B$.

• This idea can be generalized to higher dimensions. However, we restrict here to 2D only.

Incidence

• A point either lies on a line or it does not.

• If a point $A$ lies on a line $l$, denote $l\circ A$.

• For convenience, we also denote it as $A\circ l$.

• We have $A\circ l=l\circ A$

Projective Point and Line

• Projective Point

  • Exactly one line passes through two distinct points.
  • Denote join($A$, $B$) or simply $AB$ as a line joined by $A$ and $B$.
  • We have:
    • $AB$ = $BA$
    • $AB\circ A$ and $AB\circ B$ are always true.

• Projective Line

  • Exactly one point met by two distinct lines.
  • Denote meet($l$, $m$) or simply $lm$ as a point met by $l$ and $m$.
  • We have:
    • $lm$ = $ml$
    • $lm\circ l$ and $lm\circ m$ are always true.

• Duality: "Point" and "Line" are interchangable here.

• "Projective geometry is all geometry." (Arthur Cayley)

Example 1: Euclidean Geometry

• Point: projection of a 3D vector $p=[x,y,z]$ onto a 2D plane $z=1$: $$(x^{\prime },y^{\prime })=(x/z,y/z)$$

• $[\alpha x,\alpha y,\alpha z]$ for all $\alpha \ne 0$ represents the same point.

• For instance, $[1,5,6]$ and $[-10,-50,-60]$ represent the same point $(1/6,5/6)$

• $p_{\infty }=[x,y,0]$ is a point at infinity.

• Line: $a{x}^{\prime }+b{y}^{\prime }+c=0$, denoted by a vector $[a,b,c]$.

• $[\alpha a,\alpha b,\alpha c]$ for all $\alpha \ne 0$ represents the same line.

• $l_{\infty }=[0,0,1]$ is the line at infinity.

• $[0,0,0]$ is not a valid point or line.

Euclidean 2D plane from 3D vector

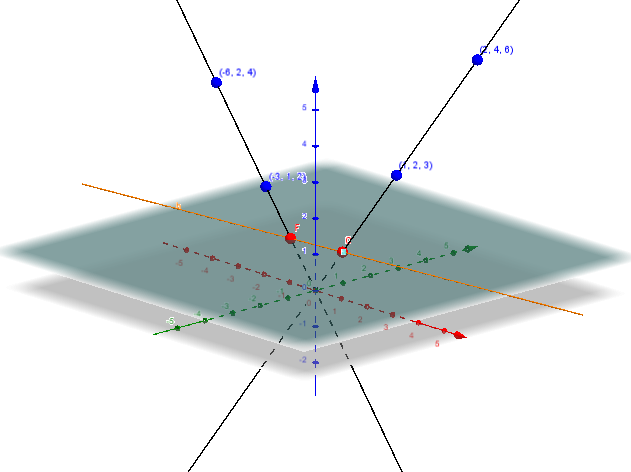{#fig:euclidean}

Calculation by Vector Operations

• Let $v_1=[x_1,y_1,z_1]$ and $v_2=[x_2,y_2,z_2]$.
  • Dot product $v_1\cdot v_2$ = $v_1^{\mathsf{T}}{v}_2$ = $x_1{x}_2+y_1{y}_2+z_1{z}_2$.
  • Cross product $v_1\times v_2$ = $[y_1{z}_2-z_1{y}_2,-x_1{z}_2+z_1{x}_2,x_1{y}_2-y_1{x}_2]$
• Then, we have:
  • $A\circ a$ precisely when $[A]\cdot [a]=0$
  • Join of two points: $[AB]$ = $[A]\times [B]$
  • Meet of two lines: $[lm]$ = $[l]\times [m]$
  • $A=B$ precisely when $[A]\times [B]=[0,0,0]$

Examples

• The linear equation that joins the point $(1/2,3/2)$ and $(4/5,3/5)$ is $[1,3,2]\times [4,3,5]$ = $[9,3,-9]$, or $9x+3y-9=0$, or $3x+y=3$.

• The point $(1/2,3/2)$ lies on the line $3x+y=3$ because $[1,3,2]\cdot [3,1,-3]$ = $0$.

• Exercise: Calculate the line equation that joins the points $(5/8,7/8)$ and $(-5/6,1/6)$.

🐍 Python Code (pg_object)

class pg_object(np.ndarray):
    @abstractmethod
    def dual(self):
        """abstract method"""
        pass

    def __new__(cls, inputarr):
*        obj = np.asarray(inputarr).view(cls)
        return obj

    def __eq__(self, other):
        if type(other) is type(self):
            return (np.cross(self, other) == 0).all()
        return False

    def __ne__(self, other):
        return not self.__eq__(other)

    def incident(self, l):
        return not self.dot(l)

    def __mul__(self, other):
        T = self.dual()
        return T(np.cross(self, other))

🐍 Python Code (pg_point and pg_line)

class pg_point(pg_object):
    def __new__(cls, inputarr):
        obj = pg_object(inputarr).view(cls)
        return obj

    def dual(self):
        return pg_line

class pg_line(pg_object):
    def __new__(cls, inputarr):
        obj = pg_object(inputarr).view(cls)
        return obj

    def dual(self):
        return pg_point

def join(p, q):
    assert isinstance(p, pg_point)
    return p * q

def meet(l, m):
    assert isinstance(l, pg_line)
    return l * m

🐍 Python Code (Example)

from __future__ import print_function
from pprint import pprint
import numpy as np

if __name__ == "__main__":
    p = pg_point([1, 3, 2])
    q = pg_point([4, 3, 5])
    print(join(p, q))

    l = pg_line([5, 7, 8])
    m = pg_line([-5, 1, 6])
    print(meet(l, m))

    p = pg_point([1-2j, 3-1j, 2+1j]) # complex number
    q = pg_point([-2+1j, 1-3j, -1-1j])
    assert p.incident(p*q)

Example 2: Perspective View of Euclidean Geometry

• It turns out that we can choose any line in a plane as the line of infinity.

{#fig:euclidean2}

Example 3: Spherical/Elliptic Geometry

• Surprisingly, the vector notations and operators can also represent other geometries, such as spherical/Elliptic geometry.

• "Point": projection of the 3D vector $[x,y,z]$ onto the unit sphere. $$(x^{\prime },y^{\prime },z^{\prime })=(x/r,y/r,z/r)$$ where $r^2=x^2+y^2+z^2$.

• Here, the two points on the opposite poles are considered to be the same point.

• "Line": $[a,b,c]$ represents the great circle intersecting the unit sphere and the plane $ax+by+cz=0$.

• The $[x,y,z]$ are called Homogeneous Coordinates.

• Here, the coordinates can be integer numbers, rational numbers (the ratio of two integers), real numbers, complex numbers, or finite field numbers, or even polynomial functions.

Spherical Geometry from 3D vector

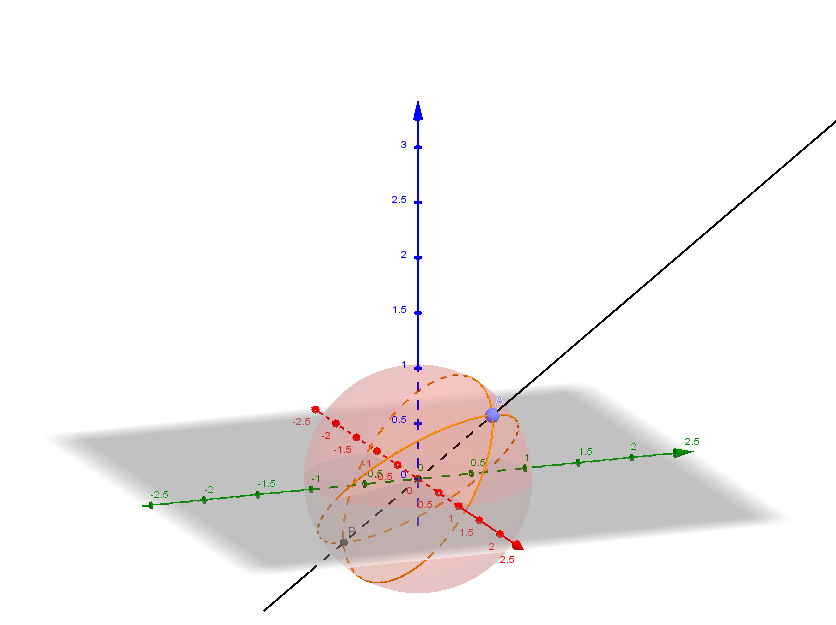{#fig:sphere}

Example 4: Hyperbolic Geometry from 3D vector

• A velocity "point": projection of a 3D vector $[p]=[x,y,t]$ onto 2D plane $t=1$: $$(v_x,v_y)=(x/t,y/t)$$

Counterexamples

• In some quorum systems, two "lines" are allowed to meet at more than one point. Therefore, it is a projective geometry only in very special cases.

• In some systems, the line from $A$ to $B$ is not the same as the line from $B$ to $A$, so they cannot form a projective geometry.

• "Symmetry" is an important keyword in projective geometry.

Number systems

• Integers ($\mathbb{Z}$):
  • e.g. $0,1,2,3,\dots ,-1,-2,-3,\dots$
  • discrete, more computationally efficient.
• Rational numbers ($\mathbb{Q}[\mathbb{Z}]$):
  • e.g. $0/1,2/3,-1/3,1/0$ (i.e. infinity)
  • Multiplication/division is simpler than addition/subtraction
• Real numbers ($\mathbb{R}$):
  • e.g. $0.3$, $2^{1/2}$, $\pi$
  • May induce round-off errors.
• Finite field, $GF(n)$, where $n$ is a prime number (e.g. $2,3,5,7,11,13$) or prime powers (e.g. $4=2^2,8=2^3,9=3^2$).
  • Used in Coding Theory

Number systems (cont'd)

• Complex numbers ($\mathbb{C}$):

  • e.g. $1+\pi i$, $1-3\pi i$
  • Besides the identity (the only automorphism of the real numbers), there is also the automorphism $\tau$ that sends $x+iy$ to $x-iy$ such that $\tau (\tau (x))=x$.

• Complex numbers over integers ($\mathbb{C}[\mathbb{Z}]$)

  • e.g. $1+2i$, $1-2i$
  • are also known as Gaussian integers.

• Complex numbers over rational numbers ($\mathbb{C}[\mathbb{Q}]$)

• Projective Geometry can work on all these number systems.

• In fact, Projective Geometry can work on any field. Moreover, multiplicative inverse operations are not required.

• No "Continuity" is assumed in Projective Geometry.

Example 4: Poker Card Geometry

• Even "coordinates" is not necessary for projective geometry.

• Consider the poker cards in @tbl:poker_card:

  • For example, meet($l_2,l_5$) = 5, join(J, 4) = $l_8$.

• We call this Poker Card Geometry here.

Table

$l_1$ $l_2$ $l_3$ $l_4$ $l_5$ $l_6$ $l_7$ $l_8$ $l_9$ $l_{10}$ $l_{11}$ $l_{12}$ $l_{13}$

A 2 3 4 5 6 7 8 9 10 J Q K

2 3 4 5 6 7 8 9 10 J Q K A

4 5 6 7 8 9 10 J Q K A 2 3

10 J Q K A 2 3 4 5 6 7 8 9

: Poker Card Geometry {#tbl:poker_card}

Finite projective plane

• Yet we may assign the homogeneous coordinate to a finite projective plane where the vector operations are in a finite field.

• E.g. the poker card geometry is a finite projective plane of order 3.

• The smallest finite projective plane (order 2) contains only 7 points and 7 lines.

• If the order is prime or prime powers, then we can easily construct the finite projective plane via finite fields and homogeneous coordinates.

• In 1989, the nonexistence of finite projective plane of order 10 was proved . The proof took the equivalent of 2000 hours on a Cray 1 supercomputer.

• The existence of many other higher order finite projective planes remains an open question.

Not covered in this work

• Unless specifically mentioned, we will not discuss finite projective plane further more.

• Although coordinate systems are not a requirement for general projective geometry, practically all examples we deal with have homogeneous coordinates. The proofs of all theorems are based on the assumption of homogeneous coordinates.

Basic Properties

Collinear, Concurrent, and Coincidence

• If all three points lie on the same line, they are said to be collinear.

• If all three lines intersect at the same point, they are called concurrent.

• Denote the coincidence relationship as coI($A,B,C$).

• coI($A,B,C$) is true precisely when $AB\circ C$ is true.

• Similarly, coI($a,b,c$) is true precisely when $ab\circ c$ is true.

• In general, coI($A_1,A_2,\dots ,A_n$) is true precisely when $A_1{A}_2\circ X$ is true for all $X$ in the remaining points $A_3,A_4,\dots ,A_n$.

• Unless otherwise mentioned, $ABCD\dots$ is assumed to be coincide, while $\{ABCD\dots \}$ is assumed to coincide with none of the three.

Parameterize a line

• The points on a line $AB$ can be parameterized by $\lambda [A]+\mu [B]$, with $\lambda$ and $\mu$ are not both zero.

• For integer coordinates, to show that $\lambda [A]+\mu [B]$ can span all integer points on the line, we give the exact expression of $\lambda /\mu$ for a point $C$ as follows.

• Let $l=[C]\times ([A]\times [B])$.

• Then $$\lambda [A]+\mu [B]=(l^{\mathsf{T}}[B])[A]-(l^{\mathsf{T}}[A])[B]$$

🐍 Python Code

def coincident(p, q, r):
    return r.incident(p * q)

def coI_core(l, Lst):
    for p in Lst:
        if not l.incident(p):
            return False
    return True

def coI(p, q, *rest):
    assert p != q
    return coI_core(p*q, rest )

# Note: `lambda` is a preserved keyword in python
def plucker(lambda1, p, mu1, q):
    T = type(p)
    return T(lambda1 * p + mu1 * q)

Pappus' Theorem

• Theorem (Pappus): Given two lines $ABC$ and $DEF$. Let $G$=meet($AE,BD$), $H$=meet($AF,CD$), and $I$=meet($BF,CE$). Then $G,H,I$ are collinear.

• Sketch of the proof:

  • Let $[C]={\lambda }_1[A]+{\mu }_1[B]$.
  • Let $[F]={\lambda }_2[D]+{\mu }_2[E]$.
  • Express $[G],[H],[I]$ in terms of $[A],[B],{\lambda }_1,{\mu }_1,{\lambda }_2,{\mu }_2$.
  • Simplify the expression $[G]\cdot ([H]\times [I])$ and conclude that it is equal to 0 (we may use the Python's symbolic package for the calculation).

• Exercise: verify that this theorem holds for 3, 6, Q on $l_3$ and 8, 9, J on $l_8$ in the poker card geometry.

🐍 Python Code for the Proof

import sympy
sympy.init_printing()
pv = sympy.symbols("p:3", integer=True)
qv = sympy.symbols("q:3", integer=True)
lambda1, mu1 = sympy.symbols("lambda1 mu1", integer=True)
p = pg_point(pv); q = pg_point(qv)
r = plucker(lambda1, p, mu1, q)
sv = sympy.symbols("s:3", integer=True)
tv = sympy.symbols("t:3", integer=True)
lambda2, mu2 = sympy.symbols("lambda2 mu2", integer=True)
s = pg_point(sv); t = pg_point(tv)
u = plucker(lambda2, s, mu2, t)
G = (p * t) * (q * s)
H = (p * u) * (r * s)
I = (q * u) * (r * t)
ans = np.dot(G, H * I)
ans = sympy.simplify(ans)
print(ans) # get 0

An instance of Pappus' theorem

{#fig:pappus}

Another instance of Pappus' theorem

{#fig:pappus2}

Triangles and Trilaterals

• If three points $A$, $B$, and $C$ are not collinear, they form a triangle, denoted as $\{ABC\}$.

• If three lines $a$, $b$, and $c$ are not concurrent, they form a trilateral, denoted as $\{abc\}$.

• Triangle $\{ABC\}$ and trilateral $\{abc\}$ are dual if $A=bc$, $B=ac$ and $C=ab$.

🐍 Python Code (II)

def tri(T):
    a1, a2, a3 = T
    l1 = a2 * a3
    l2 = a1 * a3
    l3 = a1 * a2
    return l1, l2, l3

def tri_func(func, T):
    a1, a2, a3 = T
    m1 = func(a2, a3)
    m2 = func(a1, a3)
    m3 = func(a1, a2)
    return m1, m2, m3

An example of triangle and trilateral

{#fig:triangle}

Projectivities and Perspectivities

Projectivities

• An ordered set $(A,B,C)$ (whether collinear or not) is called a projective of a concurrent set $abc$ precisely when $A\circ a$, $B\circ b$ and $C\circ c$.

• Denote this as $(A,B,C)$ $⊼$ $abc$.

• An ordered set $(a,b,c)$ (whether concurrent or not) is called a projective of a collinear set $ABC$ precisely when $A\circ a$, $B\circ b$ and $C\circ c$.

• Denote this as $(a,b,c)$ $⊼$ $ABC$.

• If each ordered set is coincident, we may write:

  • $ABC$ $⊼$ $abc$ $⊼$ $A^{\prime }{B}^{\prime }{C}^{\prime }$
  • Or simply write $ABC$ $⊼$ $A^{\prime }{B}^{\prime }{C}^{\prime }$

Perspectivities

• An ordered set $(A,B,C)$ is called a perspectivity of an ordered set $(A^{\prime },B^{\prime },C^{\prime })$ precisely when $(A,B,C)$ $⊼$ $abc$ and $(A^{\prime },B^{\prime },C^{\prime })$ $⊼$ $abc$ for some concurrent set $abc$.

• Denote this as $(A,B,C)$ $⩞$ $(A^{\prime },B^{\prime },C^{\prime })$.

• An ordered set $(a,b,c)$ is called a perspectivity of an ordered set $(a^{\prime },b^{\prime },c^{\prime })$ precisely when $(a,b,c)$ $⊼$ $ABC$ and $(a^{\prime },b^{\prime },c^{\prime })$ $⊼$ $ABC$ for some collinear set $ABC$.

• Denote this as $(a,b,c)$ $⩞$ $(a^{\prime },b^{\prime },c^{\prime })$.

An instance of perspectivity

{#fig:perspec}

Another instance of perspectivity

{#fig:perspec2}

Perspectivity

• Similar definition for more than three points:
  • $(A_1,A_2,A_3,\dots ,A_n)$ $⩞$ $(A_1^{\prime },A_2^{\prime },A_3^{\prime },\dots ,A_n^{\prime })$.
• To check perspectivity:
  • First construct a point $O$ := meet($A_1{A}_1^{\prime },A_2{A}_2^{\prime }$).
  • For the rest of the points, check if $X,X^{\prime },O$ are collinear.
• Note that $(A,B,C)$ $⩞$ $(D,E,F)$ and $(D,E,F)$ $⩞$ $(G,H,I)$ does not imply $(A,B,C)$ $⩞$ $(G,H,I)$.

🐍 Python Code (III)

def persp(L, M):
    if len(L) != len(M):
        return False
    if len(L) < 3:
        return True
    [pL, qL] = L[0:2]
    [pM, qM] = M[0:2]
    assert pL != qL
    assert pM != qM
    assert pL != pM
    assert qL != qM
    O = (pL * pM) * (qL * qM)
    for rL, rM in zip(L[2:], M[2:]):
        if not O.incident(rL * rM):
            return False
    return True

Desargues's Theorem

• Theorem (Desargues): Let the trilateral $\{abc\}$ be the dual of the triangle $\{ABC\}$ and the trilateral $\{a^{\prime }{b}^{\prime }{c}^{\prime }\}$ be the dual of the triangle $\{A^{\prime }{B}^{\prime }{C}^{\prime }\}$. Then $\{ABC\}$ $⩞$ $\{A^{\prime }{B}^{\prime }{C}^{\prime }\}$ if and only if $\{abc\}$ $⩞$ $\{a^{\prime }{b}^{\prime }{c}^{\prime }\}$.

• Sketch of the proof:

  • Let $O$ be the perspective point.
  • Let $[A^{\prime }]={\lambda }_1[A]+{\mu }_1[O]$.
  • Let $[B^{\prime }]={\lambda }_2[B]+{\mu }_2[O]$.
  • Let $[C^{\prime }]={\lambda }_3[C]+{\mu }_3[O]$.
  • Let $[G]$ = $([A]\times [B])\times ([A^{\prime }]\times [B^{\prime }])$
  • Let $[H]$ = $([B]\times [C])\times ([B^{\prime }]\times [C^{\prime }])$
  • Let $[I]$ = $([A]\times [C])\times ([A^{\prime }]\times [C^{\prime }])$
  • Express $[G],[H],[I]$ in terms of $[A],[B],[C],[O],{\lambda }_1,{\mu }_1,{\lambda }_2,{\mu }_2,{\lambda }_3,{\mu }_3$.
  • Simplify the expression $[G]\cdot ([H]\times [I])$ and find that it is equal to 0. (we may use the Python's symbolic package for the calculation.)
  • Due to the duality, the only-if part can be proved using the same technique.

🐍 Python Code for the Proof (II)

# Define symbol points p, q, s, t as before
# Define symbol lambda1, mu1, lambda2, mu2 as before
# ...
lambda3, mu3 = sympy.symbols("lambda3 mu3", integer=True)
p2 = plucker(lambda1, p, mu1, t)
q2 = plucker(lambda2, q, mu2, t)
s2 = plucker(lambda3, s, mu3, t)
G = (p * q) * (p2 * q2)
H = (q * s) * (q2 * s2)
I = (s * p) * (s2 * p2)
ans = np.dot(G, H * I)
ans = sympy.simplify(ans)
print(ans) # get 0

An instance of Desargues' theorem

{#fig:desargues}

Another instance of Desargues' theorem

{#fig:desargues2}

Projective Transformation

• Given a function $\tau$ that transforms a point $A$ into another point $\tau (A)$.

• If $A$, $B$, and $C$ are collinear and we always have $\tau (A)$, $\tau (B)$, and $\tau (C)$ collinear. Then the function $\tau$ is called a projective transformation.

• In Homogeneous coordinates, a projective transformation is any non-singular matrix multiplied by a vector.

Quadrangles and Quadrilateral Sets

• Given four points $P$, $Q$, $R$ and $S$, if none of three are collinear, they form a quadrangle, denoted as $\{PQRS\}$.

• Note that the quadrangle here can be either convex or self-intersecting.

• In total, there are six lines formed by $\{PQRS\}$.

• Suppose they meet another line $l$ at $A,B,C,D,E,F$, where

  • $A$ = meet($PQ,l$), $D$ = meet($RS,l$)

  • $B$ = meet($QR,l$), $E$ = meet($PS,l$)

  • $C$ = meet($PR,l$), $F$ = meet($QS,l$)

• We call these six points a quadrilateral set, denoted as $(AD)(BE)(CF)$.

Quadrilateral set

{#fig:quad_set}

Another quadrilateral set

{#fig:quad_set2}

Harmonic Sets

• In a quadrilateral set $(AD)(BE)(CF)$, if $A=D$ and $B=E$, then it is called a harmonic set.

• The Harmonic relation is denoted by $H(AB,CF)$.

• Then $C$ and $F$ is called a harmonic conjugate.

• Theorem: If $ABCF$ $⊼$ $abcd$, then $H(AB,CF)=H(ab,cf)$.

• In other words, projectivity preserves harmonic relation.

• Theorem: If $ABCF$ $⩞$ $A^{\prime }{B}^{\prime }{C}^{\prime }{F}^{\prime }$, then $H(AB,CF)=H(A^{\prime }{B}^{\prime },C^{\prime }{F}^{\prime })$.

• In other words, perspectivity preserves harmonic relation.

Basic metric between point and line

• A basic metric between $p$ and $l$, denoted by $p\cdot l$ (inner product):

  • $p\cdot l$ can be positive, negative, and zero.

  • $p\cdot l=0$ precisely when $p$ lies on $l$.

Cross Ratio

• Given a line incident with $ABCD$. Choose an arbitrary point $O$ that is not on that line.

• The cross ratio is defined as:

  $$R(A,B;C,D)=(OA\cdot C)(OB\cdot D)/(OA\cdot D)(OB\cdot C)$$

• Note: the cross ratio does not depend on what $O$ is chosen.

🐍 Python Code (IV)

from fractions import Fraction
import numpy as np

def ratio_ratio(a, b, c, d):
    if isinstance(a, (int, np.int64)):
        return Fraction(a, b) / Fraction(c, d)
    return (a * d) / (b * c)

def x_ratio(A, B, l, m):
    dAl = A.dot(l)
    dAm = A.dot(m)
    dBl = B.dot(l)
    dBm = B.dot(m)
    return ratio_ratio(dAl, dAm, dBl, dBm)

def R(A, B, C, D):
    O = (C*D).aux()
    return x_ratio(A, B, O*C, O*D)

Polarities

• A polarity is a projective correlation of period 2.

• We call $a$ the polar of $A$, and $A$ the pole of $a$.

• Denote $a=A^{\perp }$ and $A=a^{\perp }$.

• Except for the degenerate cases, $A=(A^{\perp }{)}^{\perp }$ and $a=(a^{\perp }{)}^{\perp }$.

• It may happen that $A$ is incident with $a$ so that each is self-conjugate.

• The locus of self-conjugate points defines a conic. However, polarity is a more general concept than conics, because some polarities may have no self-conjugate points (or their self-conjugate points are complex).

The Use of a Self-Polar triangle

• Any projective correlation that relates three vertices of one triangle to their respective opposite sides is a polarity.

• Thus, any triangle $\{ABC\}$, any point $P$ not on a side, and any line $p$ not throughout a vertex, determine a definite polarity $(ABC)(Pp)$.

The Conic

• Historically ellipse (including circle), parabola, and hyperbola.

• The locus of self-conjugate points is a conic.

• Their polars are its tangents.

• Any other line is called a secant or a nonsecant according to whether it meets the conic twice or not at all, i.e., according to whether the involution of conjugate points on it is hyperbolic or elliptic.

• Note: Intersecting a conic with a line may result of an irrational intersection point.

Construct the polar of a point using a conic

• To construct the polar of a given point $C$, not on the conic, draw any two secants $PQ$ and $RS$ through $C$; then the polar joins the two points meet($QR,PS$) and meet($RP,QS$).

Example of constructing the polar of a point

\begin{figure}[hp]
\centering
\input{figs/pole2polar.tikz}
\caption{Example of constructing the polar of a point}
\end{figure}

Another example of constructing the polar of a point

\begin{figure}[hp]
\centering
\input{figs/pole2polar2.tikz}
\caption{Another example of constructing the polar of a point}
\end{figure}

Construct the pole from a line

• To construct the pole of a given secant $a$, draw the polars of any two points on the line; then the common point of two polars is the pole of $a$.

Constructing the pole of a line

\begin{figure}[hp]
\centering
\input{figs/polar2pole.tikz}
\caption{Constructing the pole of a line}
\end{figure}

Construct the tangent of a point on a conic

• To construct the tangent at a given point $P$ on a conic, join $P$ to the pole of any secant through $P$.

Example of construct the tangent of a point on a conic

\begin{figure}[hp]
\centering
\input{figs/tangent.tikz}
\caption{Construct the tangent of a point on a conic}
\end{figure}

Another example of constructing the tangent of a point on a conic

\begin{figure}[hp]
\centering
\input{figs/tangent2.tikz}
\caption{Another example of constructing the tangent of a point on a conic}
\end{figure}

Pascal's Theorem

• If a hexagon is inscribed in a conic, the three pairs of opposite sides meet in collinear points.

An instance of Pascal' theorem

{#fig:pascal}

Another instance of Pascal' theorem

{#fig:pascal2}

Backup

melpon.org

Cayley-Klein geometry

👋 Introduction

🔑 Key points

• The gravitational/electromagnetic force between two objects is inversely proportional to the square of their distance.

• Distances and angles may be powerful for oriented measures. But quadrance and spread are more energy saving for non-oriented measures.

• Euclidean Geometry is a degenerate case.

Cayley-Klein Geometry

• Projective geometry can be further categorized by polarities.

• Except for degenerate cases, $(A^{\perp }{)}^{\perp }=A$ and $(a^{\perp }{)}^{\perp }=a$

• A fundamental cone $\mathcal{F}=(\mathbf{A},\mathbf{B})$ is defined by a pole/polar pair such that $[A^{\perp }]=\mathbf{A}\cdot [A]$ and $[a^{\perp }]=\mathbf{B}\cdot [a]$.

• To visualize Cayley-Klein Geometry, we may project the objects onto the 2D plane.

• In hyperbolic geometry, the projection of the fundamental cone onto the 2D plane is a unit circle, the so-called null circle. The distance and angle measurement can be negative outside the null circle.

• We can think of Euclidean geometry as a hyperbolic geometry in which the null circle is expanded toward infinity.

• In this section, we use the vector notation $p=[A]$ and $l=[a]$.

Fundamental Cone with pole and polar

{#fig:F}

Examples

• Let $p=[x,y,z]$ and $l=[a,b,c]$

• Hyperbolic geometry:

  • $\mathbf{A}\cdot p\equiv [x,y,-z]$
  • $\mathbf{B}\cdot l\equiv [a,b,-c]$

• Elliptic geometry:

  • $\mathbf{A}\cdot p\equiv [x,y,z]$
  • $\mathbf{B}\cdot l\equiv [a,b,c]$

• Euclidean geometry (degenerate conic):

  • $\mathbf{A}\cdot p\equiv [0,0,z]$
  • $\mathbf{B}\cdot l\equiv [a,b,0]$

• psuedo-Euclidean geometry (degenerate conic):

  • $\mathbf{A}\cdot p\equiv [0,0,z]$
  • $\mathbf{B}\cdot l\equiv [a,-b,0]$

]

Examples (cont'd)

• Perspective view of Euclidean geometry (degenerate conic):
  • Let $l$ be the line of infinity.
  • Let $p$ and $q$ are two complex conjugate points on $l$. Then
  • $\mathbf{A}\equiv l\cdot l^T$ (outer product)
  • $\mathbf{B}\equiv p\cdot q^T+q\cdot p^T$

Orthogonality

• A line $l$ is said to be perpendicular to a line $m$ if $l^{\perp }$ lies on $m$, i.e., $m^{\mathsf{T}}\mathbf{B}l=0$.

• To find a perpendicular line of $l$ that passes through $p$, join $p$ to the pole of $l$, i.e., join($p,l^{\perp }$). We call this the altitude line of $l$.

• For duality, a point $p$ is said to be perpendicular to point $q$ if $q^{\mathsf{T}}\mathbf{A}p=0$.

• A similar definition can be given for altitude points.

• Note that Euclidean geometry does not have the concept of the perpendicular point because every $p^{\perp }$ is the line of infinity.

Orthocenter of triangle

• Theorem 1 (Orthocenter and ortholine). The altitude lines of a non-dual triangle meet at a unique point $O$ called the orthocenter of the triangle.

• Despite the name "center", the orthocenter may be outside a triangle.

• Theorem 2. If the orthocenter of triangle $\{ABC\}$ is $O$, then the orthocenter of triangle $\{OBC\}$ is $A$.

An instance of orthocenter theorem

{#fig:orthocenter}

An instance of Theorem 2

{#fig:orthocenter2}

Involution

• Involution is closely related to geometric reflection.

• The defining property of an involution $\tau$ is that for every point $p$, $\tau (\tau (p))=p$.

• Theorem: Let $\tau$ be an involution. Then

  1. there is a line $m$ for which $\tau (p)=p$ for every poiny $p$ incident with $m$.
  2. there is a point $o$ for which $\tau (l)=l$ for every line $l$ incident with $o$.

• We call the line $m$ the mirror and the point $o$ the center of the involution.

• If $o$ is at the line of infinity (Euclidean Geometry), then we get an undistorted Euclidean line reflection on $m$.

• If we choose $o=m^{\perp }$, then the fundamental cone is invariant.

Involution (cont'd)

• Theorem: The point transformation matrix $T$ of the projective involution $\tau$ with center $o$ and mirror $m$ is given by $$(o^{\mathsf{T}}m)\mathrm{I}-2o{m}^{\mathsf{T}}$$

• In other words, $T\cdot p$ = $(o^{\mathsf{T}}m)p-2(m^{\mathsf{T}}p)o$.

🐍 Python Code

from proj_geom import *

def is_perpendicular(l, m):
    return m.incident(dual(l))

def altitude(p, l):
    return p * dual(l)

def orthocenter(a1, a2, a3):
    t1 = altitude(a1, a2*a3)
    t2 = altitude(a2, a1*a3)
    return t1*t2

class reflect:
    def __init__(self, m, O):
        self.m = m
        self.O = O
        self.c = dot(m, O)

    def __call__(self, p):
        return pk_point(self.c, p, -2 * dot(self.m, p), self.O)

Mirror Image

{#looking-at-self}

Basic measurement

Quadrance and Spread for the general cases

• Let $\Omega (x)=x\cdot x^{\perp }$.

• $\Omega (A)=A\cdot A^{\perp }=[A{]}^{\mathsf{T}}\mathbf{A}[A]$.

• $\Omega (a)=a\cdot a^{\perp }=[a{]}^{\mathsf{T}}\mathbf{B}[a]$.

• The quadrance $q(A,B)$ between points $A$ and $B$ is: $$q(A,B)\equiv \Omega (AB)/\Omega (A)\Omega (B)$$

• The spread $s(l,m)$ between lines $l$ and $m$ is $$s(l,m)\equiv \Omega (lm)/\Omega (l)\Omega (m)$$

• Note: they are invariant to any projective transformations.

🐍 Python Code

import numpy as np
from fractions import *

def omega(l):
    return dot(l, dual(l))

def measure(a1, a2):
    omg = omega(a1*a2)
    if isinstance(omg, int):
        return Fraction(omg, omega(a1) * omega(a2))
    else:
        return omg / (omega(a1) * omega(a2))

def quadrance(a1, a2):
    return measure(a1, a2)

def spread(l1, l2):
    return measure(l1, l2)

versus raditional Distance and Angle

• Hyperbolic:
  • $q(A,B)={\sinh }^2(d(A,B))$
  • $s(l,m)={\sin }^2(\theta (l,m))$
• Elliptic:
  • $q(A,B)={\sin }^2(d(A,B))$
  • $s(l,m)={\sin }^2(\theta (l,m))$
• Euclidean:
  • $q(A,B)=d^2(A,B)$
  • $s(l,m)={\sin }^2(\theta (l,m))$

Measure the dispersion among points on the unit sphere

The usual way:

nsimplex, n = K.shape
maxd = 0
mind = 1000
for k in range(nsimplex):
  p = X[K[k,:],:]
  for i in range(n-1):
    for j in range(i+1, n):
      dot = dot(p[i,:], p[j,:])
*     q = 1.0 - dot*dot
*     d = arcsin(sqrt(q))
      if maxd < d:
        maxd = d
      if mind > d:
        mind = d
*dis = maxd - mind

A better way:

nsimplex, n = K.shape
maxd = 0
mind = 1000
for k in range(nsimplex):
  p = X[K[k,:],:]
  for i in range(n-1):
    for j in range(i+1, n):
      dot = dot(p[i,:], p[j,:])

*     q = 1.0 - dot*dot
      if maxq < q:
        maxq = q
      if minq > q:
        minq = q
*dis = arcsin(sqrt(maxq)) \
*      - arcsin(sqrt(minq))

] ]

Spread law and Thales Theorem

• Spread Law $$q_1/s_1=q_2/s_2=q_3/s_3.$$

• (Compare with the sine law in Euclidean Geometry): $$d_1/\sin {\theta }_1=d_2/\sin {\theta }_2=d_3/\sin {\theta }_3.$$

• Theorem (Thales): Suppose that $\{a_1{a}_2{a}_3\}$ is a right triangle with $s_3=1$. Then $$s_1=q_1/q_3\text{and}{s}_2=q_2/q_3$$

• Note: in some geometries, two lines being perpendicular does not imply they have a right angle ($s=1$).

Triangle proportions

• Theorem (Triangle proportions): Suppose $d$ is a point lying on the line $a_1{a}_2$. Define the quadrances $r_1\equiv q(a_1,d)$ and $r_1\equiv q(a_2,d)$, and the spreads $R_1\equiv s(a_3{a}_1,a_{3}d)$ and $R_2\equiv s(a_3{a}_2,a_{3}d)$. Then $$R_1/R_2=(s_1/s_2)(r_1/r_2)=(q_1/q_2)(r_1/r_2).$$

Midpoint and Angle Bisector

• There are two angle bisectors for two lines.
• In general geometries, There are also two midpoints for two points.
• Let $r$ be the midpoint of $p$ and $q$.
• Then $r$ = $\sqrt{\Phi (p)}q\pm \sqrt{\Phi (q)}p$.
• Let $b$ be the angle bisector of $l$ and $m$.
• Then $b$ = $\sqrt{\Phi (m)}l\pm \sqrt{\Phi (l)}m$.
• Note:
  • The midpoint could be irrational in general.
  • The midpoint could even be complex, even both points are real.
  • The bisectors of two lines are perpendicular.
  • In Euclidean geometry, the other midpoint is on the line of infinity.

Midpoint in Euclidean geometry

• Let $l$ be the line of infinity.
• $\mathbf{A}\equiv l\cdot l^T$
• $\Phi (p)$ = $p^{\mathsf{T}}\mathbf{A}p$ = $(p^{\mathsf{T}}l{)}^2$.
• Then, the midpoint $r$ = $(q^{\mathsf{T}}l)p\pm (p^{\mathsf{T}}l)q$.
• One midpoint $(q^{\mathsf{T}}l)p-(p^{\mathsf{T}}l)q$ in fact lies on $l$.

Constructing angle bisectors using a conic

1. For each line, construct the two tangents $(t_f^1,t_f^2)$ and $(t_g^1,t_g^2)$ of its intersection points with the fundamental conic to that conic.
2. The following lines are the two angle bisectors:
   • join(meet($t_f^1,t_g^1$), meet($t_f^2,t_g^2$))
   • join(meet($t_f^1,t_g^2$), meet($t_f^2,t_g^1$))

Remark: the tangents in elliptic geometry have complex coordinates. However, the angle bisectors are real objects again.

Constructing a pair of angle bisectors

{#fig:bisector}

Angle Bisector Theorem

• Let $a$, $b$, $c$ be three lines, none of which is tangent to the fundamental cone.

• Then one set of angle bisector $m_{ab}^1,m_{bc}^1,m_{ac}^1$ are concurrent.

• Furthermore, the points meet($m_{ab}^2,c$), meet($m_{bc}^2,a$), meet($m^2\ast ac,b$*) are collinear.

An instance of complete angle bisector theorem

{#fig:bisectortheorem}

Midpoint theorem

• Let $p$, $q$, $r$ be three points, none of which lies on the fundamental cone.

• Then one set of midpoints $m_{pq}^1$, $m_{qr}^1$, $m_{pr}^1$_ are collinear.

• Furthermore, the lines join($m_{pq}^2,r$), join($m_{qr}^2,p$), join($m^2\ast pr,q$*) meet at a point.

backup

> http://melpon.org/wandbox/permlink/Rsn3c3AW7Ud8E1qX

Hyperbolic/Elliptic Geometry

👋 Introduction

🔑 Key points

• In Hyperbolic Geometry,

  • two parallel lines meet outside the null circle.

  • Given a line $l$, there are more one parallel lines that pass through a point $p$.

• Notations: To distinguish with Euclidean geometry, lines are written as capital letters.

Quadrance and Spread in Hyperbolic/Elliptic geometry

• For efficiency, quadrance and spread can also be written as follows.

• The quadrance $q(a,b)$ between points $a$ and $b$ is: $$q(a,b)\equiv 1-(a\cdot b^{\perp }{)}^2/(a\cdot a^{\perp })(b\cdot b^{\perp })$$

• The spread $S(L,M)$ between lines $L$ and $M$ is $$S(L,M)\equiv 1-(L\cdot M^{\perp }{)}^2/(L\cdot L^{\perp })(M\cdot M^{\perp })$$

• Note: In Hyperbolic Geometry, the quadrance of two points inside the null circle is negative.

Relation with Traditional Distance and Angle

• Hyperbolic:

  • Distance: $$q(a,b)={\sinh }^2(d(a,b))$$
  • Angle: $$S(L,M)={\sin }^2(\theta (L,M))$$

• Elliptic:

  • Distance: $$q(a,b)={\sin }^2(d(a,b))$$
  • Angle: $$S(L,M)={\sin }^2(\theta (L,M))$$

Spread law

• Spread Law $$q_1/S_1=q_2/S_2=q_3/S_3.$$

• (Compare with the sine law in traditional Hyperbolic Geometry): $$\sinh d_1/\sin {\theta }_1=\sinh d_2/\sin {\theta }_2=\sinh d_3/\sin {\theta }_3.$$

• (Compare with the sine law in traditional Elliptic Geometry): $$\sin d_1/\sin {\theta }_1=\sin d_2/\sin {\theta }_2=\sin d_3/\sin {\theta }_3.$$

Triple formulate

• Let $a_1$, $a_2$ and $a_3$ are points with $q_1\equiv q(a_2,a_3)$, $q_2\equiv q(a_1,a_3)$ and $q_3\equiv q(a_1,a_2)$. Let $L_1$, $L_2$ and $L_3$ are lines with $S_1\equiv S(L_2,L_3)$, $S_2\equiv S(L_1,L_3)$ and $S_3\equiv S(L_1,L_2)$.

• Theorem (Triple quad formula): If $a_1$, $a_2$ and $a_3$ are collinear points then $$(q_1+q_2+q_3{)}^2=2(q_1^2+q_2^2+q_3^2)+4q_1{q}_2{q}_3$$

• Theorem (Triple spread formula): If $L_1$, $L_2$ and $L_3$ are concurrent lines then $$(S_1+S_2+S_3{)}^2=2(S_1^2+S_2^2+S_3^2)+4S_1{S}_2{S}_3.$$

Cross Law

• Theorem (Cross law) $$(S_1{S}_2{q}_3-(S_1+S_2+S_3)+2{)}^2=4(1-S_1)(1-S_2)(1-S_3).$$

• Theorem (Cross dual law) $$(q_1{q}_2{S}_3-(q_1+q_2+q_3)+2{)}^2=4(1-q_1)(1-q_2)(1-q_3).$$

• Note:

  • Given three quadrances, three spreads can be uniquely determined. Same as Euclidean Geometry.
  • Given three spreads, three quadrances can be uniquely determined. Not true in Euclidean Geometry.

Right triangles and Pythagoras

• Theorem (Pythagoras): If $L_1$ and $L_2$ are perpendicular lines ($S(L_1,L_2)=1$) then $$q_3=q_1+q_2-q_1{q}_2.$$

• Theorem (Thales): Suppose that $\{a_1{a}_2{a}_3\}$ is a right triangle with $S_3=1$. Then $S_1=q_1/q_3$ and $S_2=q_2/q_3$.

Right parallax

• Theorem (Right parallax): If a right triangle $\{a_1{a}_2{a}_3\}$ has spreads $S_1=0$, $S_2=S$ and $S_3=1$, then it will have only one defined quadrance $q_1=q$ given by $$q=(S-1)/S.$$

• We may restate this result in the form: $$S=1/(1-q).$$

Triangle proportions and barycentric coordinates

Triangle proportions

• Theorem (Triangle proportions): Suppose that $d$ is a point lying on the line $a_1{a}_2$. Define the quadrances $r_1\equiv q(a_1,d)$ and $r_1\equiv q(a_2,d)$, and the spreads $R_1\equiv S(a_3{a}_1,a_{3}d)$ and $R_2\equiv S(a_3{a}_2,a_{3}d)$. Then $$R_1/R_2=(S_1/S_2)(r_1/r_2)=(q_1/q_2)(r_1/r_2).$$

Euclidean geometry

Basic

• Line at infinity $l_{\infty }=[0,0,1]$

• Two special points $\mathrm{I}$ and $\mathrm{J}$ on $l_{\infty }$ play an important role in Euclidean Geometry:

  • $\mathrm{I}=[1,-i,0]$, $\mathrm{J}=[1,i,0]$

• $\mathbf{A}=l_{\infty }\cdot l_{\infty }^{\mathsf{T}}$

• $\mathbf{B}=\mathrm{I}\cdot {\mathrm{J}}^{\mathsf{T}}+\mathrm{J}\cdot {\mathrm{I}}^{\mathsf{T}}$

• If we choose another line $l=M\cdot l_{\infty }$ as line of infinity

Rational Trigonometry in Euclidean geometry

Notations

• To distinguish with Euclidean geometry, points are written in capital letters.

Quadrance and Spread in Euclidean geometry

• The quadrance $Q$ between points $A_1$ and $A_2$ is: $$Q=(x_1/z_1-x_2/z_2{)}^2+(y_1/z_1-y_2/z_2{)}^2$$

• The spread $s$ between lines $l_1$ and $l_2$ is: $$s=(a_1{b}_2-a_2{b}_1{)}^2/(a_1^2+b_1^2)(a_1^2+b_1^2)$$

• The cross $c$ between lines $l_1$ and $l_2$ is: $$c=1-s=(a_1{a}_2+b_1{b}_2{)}^2/(a_1^2+b_1^2)(a_1^2+b_1^2)$$

Triple formulate

• Let $A_1$, $A_2$ and $A_3$ are points with $Q_1\equiv Q(A_2,A_3)$, $Q_2\equiv Q(A_1,A_3)$ and $Q_3\equiv Q(A_1,A_2)$. Let $l_1$, $l_2$ and $l_3$ are lines with $s_1\equiv s(l_2,l_3)$, $s_2\equiv s(l_1,l_3)$ and $s_3\equiv s(l_1,l_2)$.

• Theorem (Triple quad formula): If $A_1$, $A_2$ and $A_3$ are collinear points then $$(Q_1+Q_2+Q_3{)}^2=2(Q_1^2+Q_2^2+Q_3^2)$$

• Theorem (Triple spread formula): If $l_1$, $l_2$ and $l_3$ are concurrent lines then $$(s_1+s_2+s_3{)}^2=2(s_1^2+s_2^2+s_3^2)+4s_1{s}_2{s}_3.$$

Spread Law

• Suppose that triangle $\{A_1{A}_2{A}_3\}$ form quadrances $Q_1\equiv Q(A_2,A_3)$, $Q_2\equiv Q(A_1,A_3)$ and $Q_3\equiv Q(A_1,A_2)$, and it dual trilateral $\{l_1{l}_2{l}_3\}$ form spreads $s_1\equiv s(l_2,l_3)$, $s_2\equiv s(l_1,l_3)$ and $s_3\equiv s(l_1,l_2)$. Then:

• Theorem (Spread Law) $$Q_1/s_1=Q_2/s_2=Q_3/s_3.$$

• (Compare with the sine law in Euclidean Geometry): $$d_1/\sin {\theta }_1=d_2/\sin {\theta }_2=d_3/\sin {\theta }_3.$$

Cross Law

• Theorem (Cross law) $$(Q_1+Q_2-Q_3{)}^2=4Q_1{Q}_2(1-s_3).$$

• (Compare with the Cosine law) $$d_3^2=d_1^2+d_2^2-2d_1{d}_2\cos {\theta }_3.$$

Right triangles and Pythagoras

• Suppose that $\{A_1{A}_2{A}_3\}$ is a right triangle with $s_3=1$. Then

• Theorem (Thales) $$s_1=Q_1/Q_3\text{and}{s}_2=Q_2/Q_3.$$

• Theorem (Pythagoras) $$Q_3=Q_1+Q_2.$$

Archimedes' function

• Archimedes' function $A(Q_1,Q_2,Q_3)$

  $$Ar(Q_1,Q_2,Q_3)=(Q_1+Q_2+Q_3{)}^2-2(Q_1^2+Q_2^2+Q_3^2)$$

• Non-symmetric but more efficient version: $$Ar(Q_1,Q_2,Q_3)=4Q_1{Q}_2-(Q_1+Q_2-Q_3{)}^2$$